1959年　一次　理科・衛生看護学科　[4]

次の□の中に適当な数を記入せよ。
方程式 $x=\pm a$ , $y=\pm b$ , $bx+ay=\pm c^2$ , ( $a>0$ , $b>0$ , $c>0$ ) で表わされる 6 個の直線を考える。

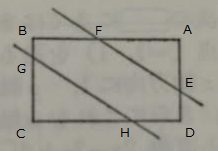
(1) これらの直線が図のように六角形を囲むための条件は $\frac{c^2}{ab}<$ (12)□

(2) その六角形の面積 A が直線 $x=\pm a$ , $y=\pm b$ で囲まれる長方形の面積の $\frac{3}{4}$ に等しいとき, $\frac{c^2}{ab}=$ (13)□

(3) $c=1$ とし, $a$ , $b$ を条件 $a^2+b^2=8$ , $a\geq b>0$ のもとで動かすとき, 六角形の面積 A が最大となるのは $a=$ (14)□, $b=$ (15)□の場合であって, そのとき A=(16)□である。

(1)
直線 $bx+ay=c^2$ は BD に平行(傾きがともに $-\frac{b}{a}$ )なので, 直線 $bx+ay=c^2$ が AB と交われば DC と交わる.
さらに, 対称性より, このとき直線 $bx+ay=-c^2$ は BC, CD と交わる.

これらのことに気づけなくても, 直線 $bx+ay=c^2$ が AB, DA と交わる条件, 直線 $bx+ay=-c^2$ が BC, CD と交わる条件の計 4 つを地道に計算すればできます.

直線 $bx+ay=c^2$ ( $x=-\frac{a}{b}y+\frac{c^2}{b}$ ) が AB と交わる条件は
[tex:-a<-\frac{a}{b}\times b+\frac{c^2}{b}0] より
$\frac{c^2}{ab}<2$

(2)
直線 $bx+ay=c^2$ と直線 $x=a$ , $y=b$ との交点 E, F の座標を求めると
$E\left(a,-b+\frac{c^2}{a}\right)$
$F\left(-a+\frac{c^2}{b},b\right)$
また, $A(a,b)$
よって, △AEF=△CGH= $\frac{1}{2}\left\{a-\left(-a+\frac{c^2}{b}\right)\right\}\left\{b-\left(-b+\frac{c^2}{a}\right)\right\}=\frac{1}{2}\left(4ab-4c^2+\frac{c^4}{ab}\right)$
六角形の面積 A は長方形の面積から △AEF と △CGH の面積の和を引いて
$A=4ab-2\times\frac{1}{2}\left(4ab-4c^2+\frac{c^4}{ab}\right)=4c^2-\frac{c^4}{ab}$
これが長方形の面積の $\frac{3}{4}$ であるから
$4c^2-\frac{c^4}{ab}=4ab\times\frac{3}{4}$
$a>0$ , $b>0$ より
$\frac{c^4}{a^2b^2}-4\frac{c^2}{ab}+3=0$
これより
$\left(\frac{c^2}{ab}-1\right)\left(\frac{c^2}{ab}-3\right)=0$
(1) より $\frac{c^2}{ab}<2$ なので $\frac{c^2}{ab}=1$

(3)
$c=1$ より
$A=4c^2-\frac{c^2}{ab}=4-\frac{1}{ab}$
ここで, $a>0$ , $b>0$ , $a^2+b^2=8$ だから, 相加・相乗平均の関係式より
$ab=\sqrt{a^2b^2}\leq\frac{a^2+b^2}{2}=4$
よって
$A=4-\frac{1}{ab}\geq4-\frac{1}{4}=\frac{15}{4}$
ゆえに, A の最大値は $\frac{15}{4}$ で, このとき $a>0$ , $b>0$ , $a^2=b^2$ , $a^2+b^2=8$ より $a=b=2$

相加・相乗平均の関係式を使うことが思いつかなくても
$a^2+b^2=8$ , $b>0$ より $b=\sqrt{8-a^2}$ だから
$A=4-\frac{1}{ab}=4-\frac{1}{\sqrt{8-a^2}}$ として,
$f(a)=\frac{1}{\sqrt{8-a^2}}$ の最小値とそのときの $a$ の値を微分して増減表を書いて調べるという方法もありますが面倒です.